Aufgabe A 2.1
Ein Klimaforscher beschreibt die Entwicklung der globalen Durchschnittstemperatur
modellhaft durch die Funktion f mit
f(t)=2,8·e0,008t-0,03t+11,1; 0≤t≤200
Dabei gibt t die Zeit in Jahren seit Beginn des Jahres 1900 und f(t) die globale Durchschnittstemperatur in Grad Celsius an. Bearbeiten Sie die folgenden Teilaufgaben anhand dieses Modells.a) Geben Sie die globale Durchschnittstemperatur zu Beginn des Jahres 1900 an.
Geben Sie die niedrigste globale Durchschnittstemperatur seit 1900 an.
In welchem Jahr wird die globale Durchschnittstemperatur 16,0 °C überschreiten?
Ermitteln Sie die momentane Änderungsrate der globalen Durchschnittstemperatur zu Beginn des Jahres 2000.
Bestimmen Sie den Mittelwert der globalen Durchschnittstemperatur im durch die Modellierung beschriebenen Zeitraum.
(4,5 VP)
b) Formulieren Sie eine Fragestellung im Sachzusammenhang, die auf die Gleichung f(t+10)-f(t)=0,5 führt.Nachdem die globale Durchschnittstemperatur ihren niedrigsten Wert erreicht hat, steigt sie immer weiter an.
Zeigen Sie, dass dieser Anstieg immer schneller verläuft.
(3,5 VP)
c) Es werden Klimaschutzmaßnahmen geplant. Greifen diese zum Zeitpunkt t0, so bleibt die momentane Änderungsrate der globalen Durchschnittstemperatur konstant bei dem Wert, der durch das Modell des Klimaforschers für t0 vorausgesagt wird.Bestimmen Sie den spätesten Zeitpunkt t0, zu dem die Maßnahmen greifen müssen, damit die globale Durchschnittstemperatur 15,7 °C bis zum Beginn des Jahres 2050 nicht überschreiten wird.
(3 VP)
d) Infolge alternativer Klimaschutzmaßnahmen kann der Verlauf der globalen Durchschnittstemperatur ab Beginn des Jahres 2020 durch beschränktes Wachstum modelliert werden.Der Graph der zugehörigen Funktion g schließt sich dabei ohne Knick an den Graphen der Funktion f an. Außerdem stellt sich nach diesem neuen Modell langfristig eine globale Durchschnittstemperatur von 16,8 °C ein.
Bestimmen Sie einen Funktionsterm von g.
(4 VP)
Aufgabe A 2.2
Für jedes a>0 ist eine Funktion fa mit fa(x)=-ax4+4ax2 gegeben.
a) Begründen Sie, dass der Graph von fa achsensymmetrisch zur y-Achse ist.
Zeigen Sie, dass die Nullstellen der Funktion fa unabhängig von a sind.
(2 VP)
b) Sowohl der Graph der Funktion g mit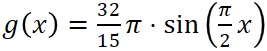
als auch der Graph von fa schließen für 0≤x≤2 eine Fläche mit der x-Achse ein.Bestimmen Sie a so, dass beide Flächen den gleichen Inhalt haben.
(3 VP)
| Downloads |
PowerPoint